Managing Sustainability

The concept of sustainable development has been gaining increasing attention because so far the impact of human development/activities on the ecosystem were not considerably realized as the human race was largely embedded in and protected by the smooth functioning of a giant biosphere of ecological networks. However, as our available energies have began to constitute a substantial portion of the ecological network, it is possible that we may start damaging our own basis for support particularly if we make changes whose impact are not clearly understood. Sustainable development has generically been defined as "the development that meets the needs of the present without compromising the ability of the future generations to meet their own needs". Most of the research work at VRI focuses on developing and enhancing technologies that ensure sustainable development.

The topic of sustainability is not limited to industrial ecology and is, perhaps, operationally and conceptually one of the most complex that modern science has faced as it involves dynamic socio-economic interactions and its effect on the overall ecosystem. The figure below presents the extension of framework from process design, to industrial ecology leading to socio-economic sustainability. At the center of this new framework is the green chemical plant engineered with clean products, clean processes, and green energy, and eco-friendly management and planning.

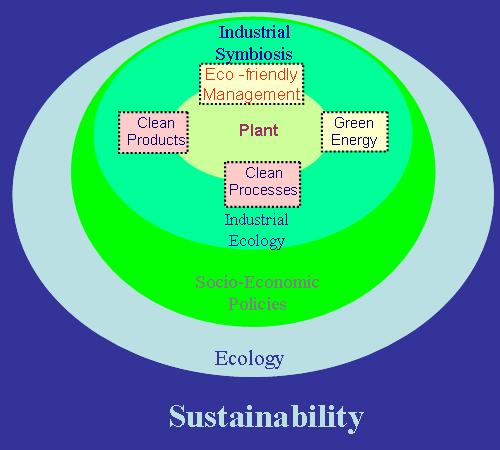
The concept of sustainability, an abstract one by its nature, has been given a mathematical representation through the use of Fisher Information (FI) so as to address the cross disciplinary nature of sustainability involving human interactions with ecosystem. FI can be conceptually considered to be a measure of the state of disorder of a system or phenomenon and thus help in evaluating sustainability. Many of the effects of human activities are often not evident immediately but manifest themselves only over a longer horizon of time and hence it becomes necessary to study the time dependent management decisions as against a time-independent approach. The theory of optimal control from systems engineering can be used to account for such inherent dynamic characteristics of natural systems. Also, the selection of control variable to maintain sustainability needs to be given sufficient attention as these control variables should be capable of being manipulated in a considerable range in reality and also need to have a significant impact on the system dynamics. A stochastic analysis based on sampling to obtain Partial Rank Correlation Coefficients (PRCC) can be employed to accomplish this task.

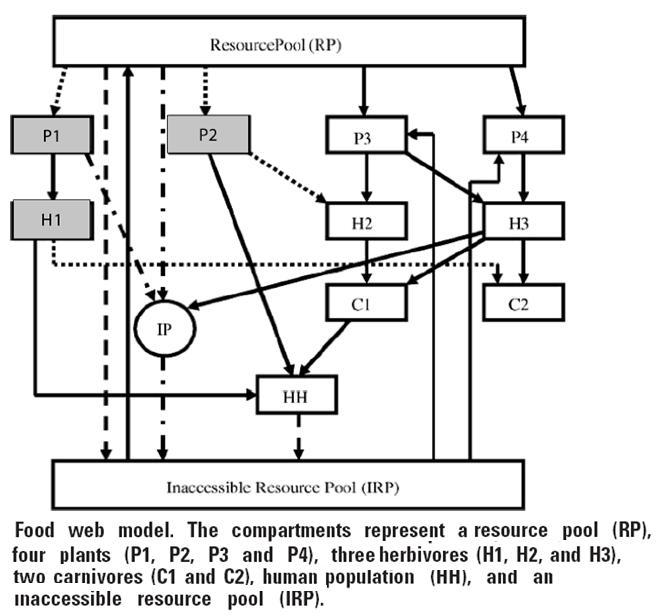
The applicability of the concepts like PRCC and FI has been demonstrated on the sustainability study of a 12-compratment food web model (shown in the figure below). An initial set of 8 variables from the model were selected as potential control variables. Subsequently, a PRCC analysis was done to prune down this set to four as these variables were more effective than the rest of the variables. The various control possibilities are ranked by evaluating their performance on different cases of the food web model with undesirable dynamics requiring external intervention are simulated. The objective is to recover the system from the disturbance in a sustainable manner, i.e. 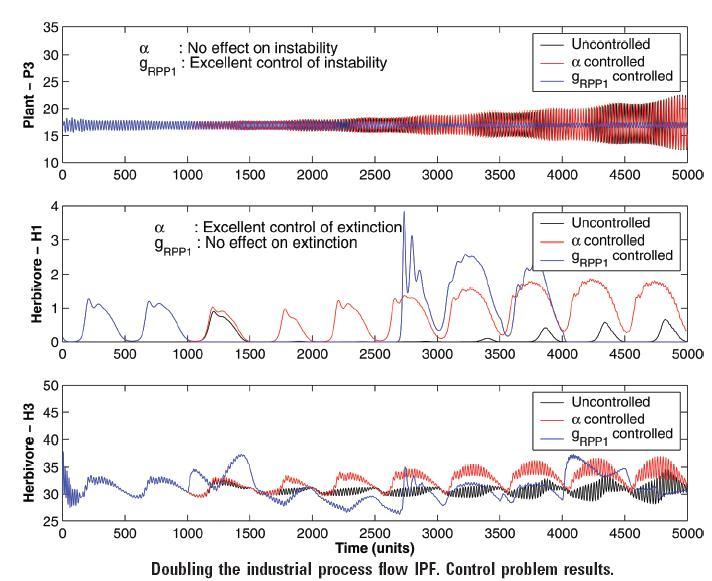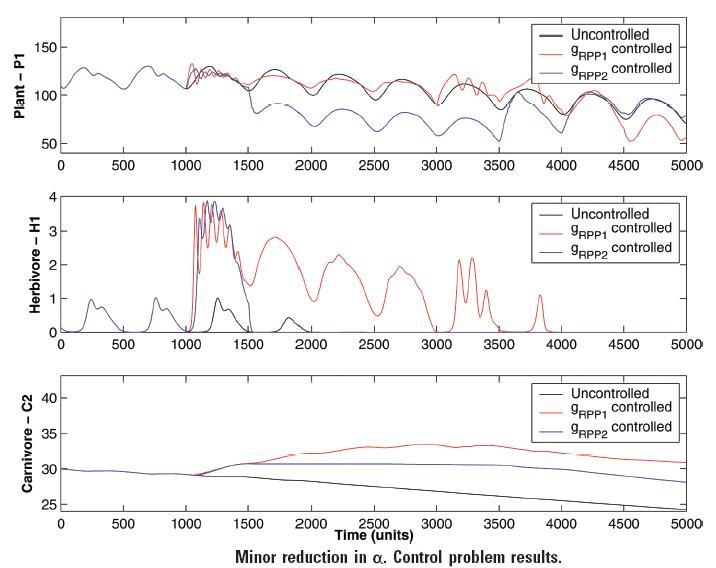to achieve dynamic stability. It was observed that some variables are more effective in controlling model instability, while others are more effective in avoiding extinction. To enhance a two step control strategy has also been proposed. In this strategy, two different single variable control problems are solved sequentially. The model is first subjected to one control action (primary control action), using one parameter as the control variable, referred to as the primary control variable (CV-1). In the next step, another control problem with a different control variable, referred to as the secondary control variable (CV-2), is solved using the primary controlled model as the starting point. The time-dependent profile of CV-1 is based on the primary control problem solution and does not change during the second control problem solution. 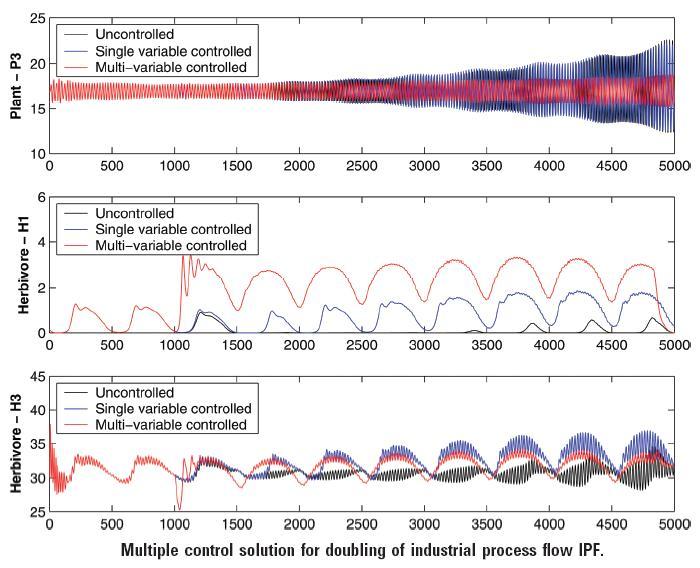The solution of the second control problem thus has time-dependent profiles for CV-1 as well as CV-2. The results indicated that the model dynamics using multiple controls are much better than those with single variable control.

Moments of the distribution resulting from the stochastic simulation become the objective function within the stochastic optimization scheme depicted in Figure 3. Expected value and/or standard deviation of the distributions are fed to the optimizer that determines the decision variables under which all the uncertain variables scenarios have to be evaluated. Naturally, the computational expenses of these schemes are high since for each policy determined by the optimizer all the scenarios of the uncertain variables need to be evaluated to obtain the distribution and its corresponding moments. Optimization under uncertainty is an important tool for water management. Efficient algorithms are required to reduce the calculation efforts; better optimization of non-linear uncertain systems (BONUS) is an excellent example. The algorithm makes use of a re-weighting scheme of the results of a single stochastic simulation involving both uncertain and decision variables to estimate the values of the objective function for different policies generated by a non-linear programming algorithm. The estimation methodology is shown in Figure 4.